Clonová čísla:
1	1,4	2	2,8	4	5,6	8	11	16	22	32	45

Expoziční časy: (zlomky sekundy)
1	2	4	8	15	30	60	125	250	500	1000	2000

Pokud budeš chtít přijít na to, proč jsou clonová čísla právě taková, musíš začít od pojmu světelnost objektivu. Objektiv je tím světelnější, čím větší má průměr vstupního otvoru, protože větším otvorem projde více světla. Zdánlivě velmi jednoduché, ale je tu malý háček, který vězí v používání objektivů o různé ohniskové vzdálenosti. Důvodem je různý stupeň zvětšení (nebo zmenšení) obrazu. Při porovnání dvou objektivů o ohniskové vzdálenosti 50mm (f1) a 100mm (f2) zjistíš, že díky lineárnímu šíření světla bude obraz vykreslený 100mm objektivem právě dvakrát větší, než obraz tvořený 50mm objektivem.

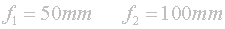
Aby byl obraz vykreslen ostře, musí být vzdálenost objektivu od roviny filmu rovna jeho ohniskové vzdálenosti. Proto musí být vzdálenost 100mm objektivu od roviny filmu právě dvakrát větší než v případě 50mm:

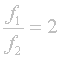
Intenzita světla ale klesá se čtvercem vzdálenosti, to je neúprosný optický zákon. Proto intenzita světla klesne čtyřikrát!

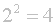
Pokud se tedy pokusíš zachovat intenzitu světla získanou 100mm objektivem na úrovni intenzity z 50mm objektivu, budeš muset zvětšit plochu vstupního otvoru 100mm objektivu právě na čtyřnásobek plochy 50mm objektivu:

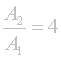
Plocha (A) se měří poněkud špatně, lepší je se podívat na to, co výše uvedená fakta znamenají pro průměr vstupního otvoru objektivu (d). Výchozím bodem je známý vzoreček pro výpočet plochy kruhu:

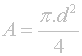
Dále musí být zachován čtyřnásobek plochy vstupního otvoru 100mm objektivu oproti 50mm objektivu, takže po dosazení vzorečků pro jednotlivé plochy A1 a A2 vznikne tato vícepatrová obluda:

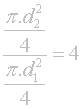
Po její úpravě je výsledek malinko snáze stravitelný - i přes zavedenou odmocninu:

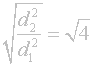
No a finální výsledek vede k jednoznačnému závěru - kolikrát zvětšíš ohniskovou vzdálenost objektivu, tolikrát musíš zvětšit průměr jeho vstupního otvoru:

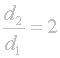
Proto může být světelnost objektivu definována jako poměr průměru vstupního otvoru objektivu k jeho ohniskové vzdálenosti. Používá se značení f/světelnost a shodná hodnota světelnosti znamená pro všechny ohniskové vzdálenosti stejnou intenzitu světla dopadajícího na světlocitlivý element (samozřejmě, že znamená zároveň různý průměr vstupního otvoru - toto je hlavní příčina, proč objektiv při narůstající ohniskové vzdálenosti nabývá i na průměru).

Zvolená výchozí hodnota řady clonových čísel je jedna, což znamená průměr vstupního otvoru o velikosti ohniska objektivu.

Další matematická šaráda vede k objasnění řady clonových čísel.

Na začátku je opět známá formulka pro výpočet plochy kruhu. Zadefinujeme dvě plochy, A1 a A2:

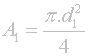
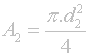
To, co je potřeba dosáhnout při jednom clonovém kroku, je snížení intenzity prošlého světla právě na polovinu. Toho se dosáhne volbou právě poloviční plochy otvoru, kterým bude procházet světlo - tedy A2 bude polovinou A1:

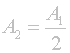
Zajímavé je opět sledovat vliv změny plochy na průměr vstupního otvoru. Po dosazení vzorečků pro výpočet plochy vznikne poměrně jednoduše řešitelný vztah:

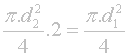
Výsledkem úpravy je poznatek, že poměr čtverců průměrů je roven žádoucí změně plochy:

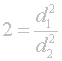
Jednoduchá úprava:

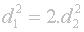
A po odmocnění je tady výsledek, který říká, že dalšího člena v řadě clonových čísel lze získat násobením (nebo dělením) předchozího odmocninou ze dvou:

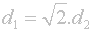
Protože objektiv označený clonovými čísly formátu 5.656854249492380195.... by zřejmě svému majiteli činil jisté technické problémy při vyhledávání žádané clony, zaokrouhlují se clonová čísla do podoby uvedené v tabulce na začátku této stránky.

Je tu ještě jeden, snad už poslední háček, skrytý ve zlomku  f/světelnost. Znamená totiž, že čím je číselná hodnota světelnosti větší, tím méně světla objektivem prochází. Totéž platí samozřejmě i pro clonová čísla.